
- #Moment of inertia of a circle given diamter how to#
- #Moment of inertia of a circle given diamter full#

#Moment of inertia of a circle given diamter how to#
How to calculate Moment of inertia of hollow circle about diametrical axis using this online calculator? To use this online calculator for Moment of inertia of hollow circle about diametrical axis, enter Outer diameter of circular section (d o) & Inner Diameter of Circular Section (d i) and hit the calculate button. The moment of inertia of a circular section of diameterd about X-axis as shown in the figure D (a) 3 ads Tid (c) 7 16 64 For Circle, through center 1. Polar moment of inertia is denoted by J symbol. Then we allow that each disk is in nitesimally thin, and contributes a mass dm: dI d 1 2 r2 dm. A disk of radius rand mass mhas moment of inertia I d 1 2 mr2 (dfor disk').

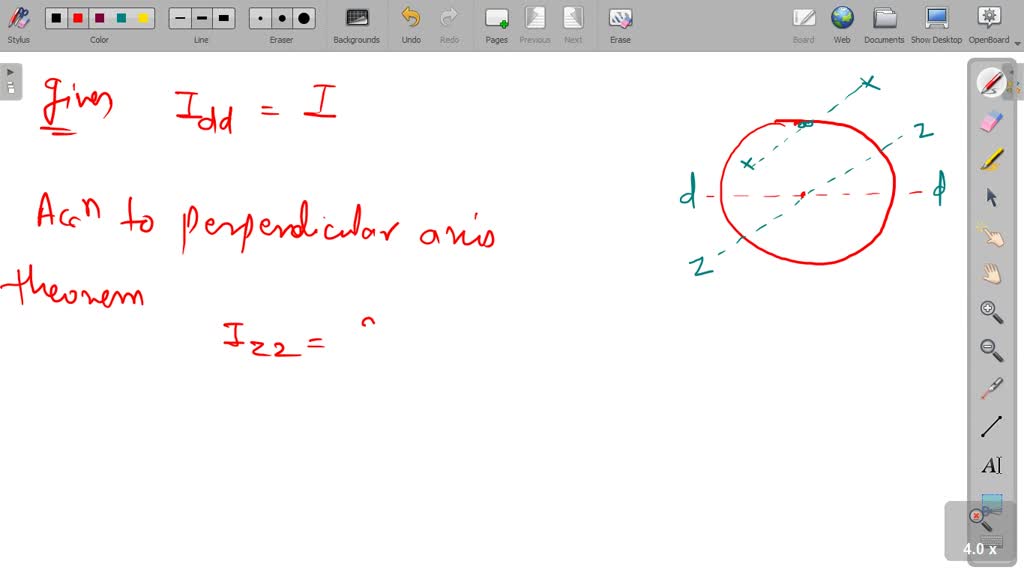
Moment of inertia of hollow circle about diametrical axis calculator uses polar_moment_inertia = ( pi/64)*( Outer diameter of circular section^4- Inner Diameter of Circular Section^4) to calculate the Polar moment of inertia, The Moment of inertia of hollow circle about diametrical axis formula is defined as the 1/64 times of product of Archimedes' constant (pi) and difference of outer diameter power raised to 4, inner diameter power raised to 4. the total moment of inertia of the cone (a stack of disks). 15.6, moment Of inertia is required to be found out. The following image provides area moment of inertia formula for few more common shapes. In a similar way, the moment of area of a pipe is given by I (D 4 -d 4 )/64 Where DPipe OD and dPipe ID. Circle with Square Cutout Section Polar Moment of Inertia Calculator. Moment of Inertia of Hollow Circular Section consider a hollow circular section as shown in Fig. The moment of inertia for a circular cross-section is given by I d 4 /64 where dDiameter of the circle. The polar moment of inertia, J, of a cross-section with respect to a polar axis. Then we calculate the circumference of circle using above mentioned formulae and print it on screen using cout.How to Calculate Moment of inertia of hollow circle about diametrical axis? Given: Diameter (d) 50 mm that moment of inertia of the circular section about an axis passing through its (d)4 x (50)4 307 x 103 rnm4 Ans. In above program, we first take radius of circle as input from user and store it in variable radius. Circumference of Circle = 2 X PI x RadiusĬout << "Circumference of circle : " << circumference The moment of inertia of a uniform cicrular disc about its diameter is. The moment of inertia of a circular ring of mass, radius about an axis perpendicular to its plane and passing through its centre is. With that, we will solve the equation below. Answer: c Explanation: Theorem of perpendicular axis stares that if IXX and IYY be the moment of inertia of a plane section about two mutually perpendicular axis X-X and Y-Y in the plane of the section then the moment of inertia of the section IZZ about the axis Z-Z, perpendicular to the plane and passing through the intersection of X-X and Y-Y is given by the formula. Moment of inertia of a thin circular plate of mass, radius about an axis passing through its diameter is.

However, the part of the circle rotating about an axis will be symmetric and the values will be equal for both the y and x-axis.
#Moment of inertia of a circle given diamter full#
C Program to calculate circumference of a circle Now if take a quarter circle, the moment of inertia relative to the x-axis and y-axis will be one quarter the moment inertia of a full circle. Let us determine the moment of inertia of small elementary circular strip about an axis ZZ which is passing through the center O of the circular section and. Moment of inertia about the x-axis: displaystyle Ix int y2, dA.


 0 kommentar(er)
0 kommentar(er)
